Помогите пожалуйста с геометрией

Question

Дан 1 ответ

nikebod313_zn · Answer 1 · 2020-06-05T17:26:43+0000

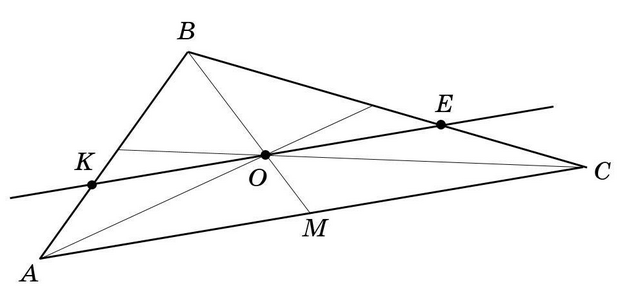
1. Пусть задан треугольник $ABC$ и прямая $a \parallel AC$ , проходящая через точку $O$ пересечения медиан треугольника $ABC$ и пересекающая стороны $AB$ и $BC$ в точках $K$ и $E$ соответственно (см. вложение). $KE = 12$ см и $S_{\bigtriangleup ABC} = 72$ см².

Три медианы треугольника пересекаются в одной точке, которая делит медианы в отношении $2:1$ , считая от вершины, поэтому $BO : OM = 2 : 1$

Пусть $k$ — коэффициент пропорциональности. Тогда $BO : OM = 2k : k$ .

Поскольку $KE \parallel AC$ , то соответствующие углы при параллельных прямых $\angle BKE = \angle BAC$ и $\angle BEK = \angle BCA$ . Следовательно, $\bigtriangleup KBE \sim \bigtriangleup ABC$ (по двум углам). Тогда все соответствующие стороны треугольников и отрезки пропорциональны.

$\dfrac{BO}{BM} = \dfrac{KE}{AC} \Rightarrow \dfrac{2k}{2k + k} = \dfrac{12}{AC} \Rightarrow AC = \dfrac{3k \cdot 12}{2k} = 18$ см

Коэффициент подобия: $k' = \dfrac{2}{3}$

Площади соответствующих подобных треугольников равны их коэффициенту подобия в квадрате:

$\dfrac{S_{\bigtriangleup KBE}}{S_{\bigtriangleup ABC}} = (k')^{2} \Rightarrow \dfrac{S_{\bigtriangleup KBE}}{72} = \left(\dfrac{2}{3} \right)^{2} \Rightarrow S_{\bigtriangleup KBE} = \dfrac{72 \cdot 4}{9} = 32$ см²

Ответ: 18 см; 32 см²

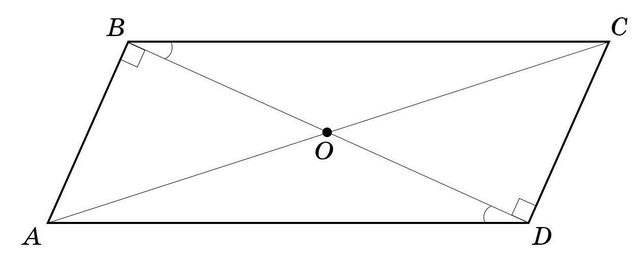
2. Пусть задан параллелограмм $ABCD$ со стороной $AD = 12$ см и диагональю $BD$ , перпендикулярной стороне $AB$ , $\angle ABC = 120^{\circ}$ , и точкой $O$ пересечения диагоналей $AC$ и $BD$ .

$\angle CBD = \angle ADB = \angle ABC - 90^{\circ} = 120^{\circ} - 90^{\circ} = 30^{\circ}$

Рассмотрим прямоугольный треугольник $ABD \ (\angle B = 90^{\circ}):$

$AB = AD \cdot \sin \angle ADB = 12 \cdot \dfrac{1}{2} = 6$ см

Следовательно, $AB = CD = 6$ см по свойству параллелограмма.

$BD = AD \cdot \cos \angle ADB = 12 \cdot \dfrac{\sqrt{3}}{2} = 6\sqrt{3}$ см

По свойству параллелограмма точка $O$ делит его диагонали на два равных отрезка, значит $BO = OD = \dfrac{BD}{2} = 3\sqrt{3}$ см и $AO= OC = \dfrac{AC}{2}$