Геометрия, 9 класс. 40 балов. Помощь!!!

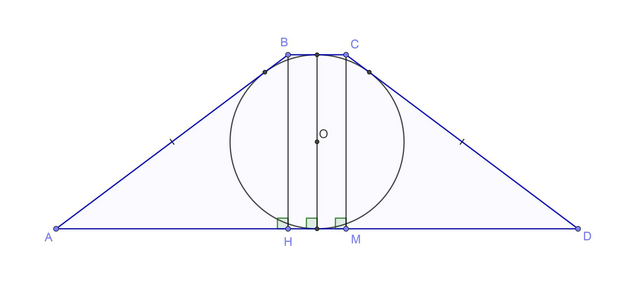
Задача: Диаметр окружности равен 9 см. Около нее описана равнобедренная трапеция, боковая сторона которой 15 см. Вычислить основания и площадь трапеции.

Решение:

Обозначим трапецию за ABCD, AD и BC — основы, AB = AD = 15 см — боковые стороны, BH = CM = d = 9 см — высоты трапеции.

Четырехугольник можно описать вокруг окружности тогда и только тогда, когда суммы длин его противоположных сторон равны:

BC+AD = AB+CD = 15+15 = 30 см

Тогда периметр трапеции:

Р = 30*2 = 60 см

AH из прямоугольного ΔABH (по т. Пифагора):

$AH=\sqrt{AB^2-BH^2} \\AH=\sqrt{15^2-9^2}=\sqrt{225-81}=\sqrt{144} =12 \:\: (cm)$