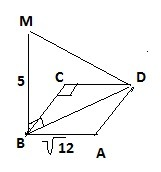
10. Сторона квадрата равна √12, тогда диагональ квадрата по теореме Пифагора ВD=√(2*√12)²=√24=2√6см
МD=√(MB²+BD²)=√(25+24)=√49=7cм.
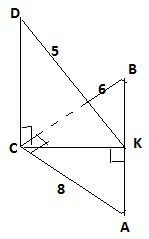
11. Из прямоугольного ΔАВС по т. Пифагора АВ=√(СВ²+СА²)=√(36+64)=10см. Перпендикуляр, опущенный из вершины прямого угла на гипотенузу делит треугольник на подобные треугольники, поэтому АВ/АС=АС/АК АК=АС²/АВ=64/10=6,4см. Используем теорему о трех перпендикулярах⇒ DC⊥ABC, DK⊥АВ, CK⊥AB,
находим СК=√(АС²-АК²)=√(64-40,96)=√23,04=4,8.
DC⊥CK⇒DC=√(DK²-CK²)=√(25-23,04)=√1.96=1,4cм..
К решению прикреплены 2 файла..