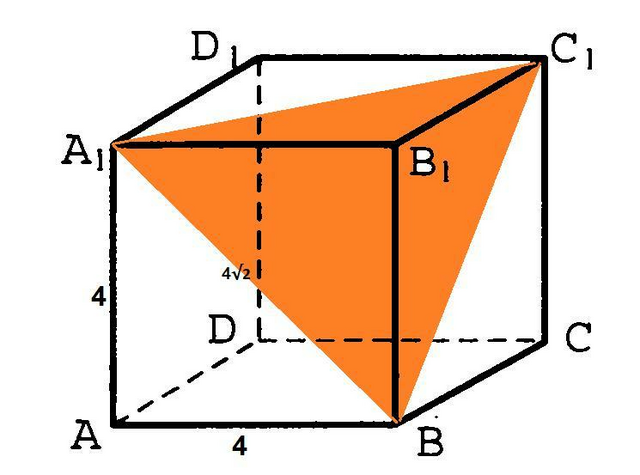
Ребро куба равно 4 см. Найти площадь сечения, образованного двумя диагоналями боковых граней, выходящих из одной вершины.
Объяснение:
Вершина В : выходят диагонали ВА₁ и ВС₁. Соединим А₁ и С₁ . В сечении получился ΔВА₁С₁-равносторонний, т.к диагонали равных квадратов равны.
ΔАВА₁-прямоугольный , по т.Пифагора ВА₁²=4²+4² , ВА₁²=2*4².
Площадь равностороннего треугольника вычисляется по формуле S=(а²√3):4.
S=(2*4²*√3):4 = 8√3 (см²)