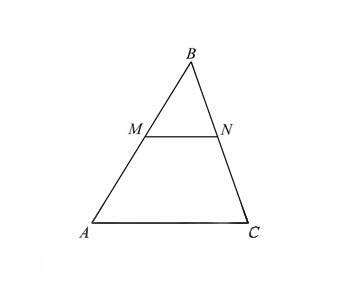
Ответ:
BN = 14
Объяснение:
Рассмотрим треугольники ABC и MBN с общим углом B. Поскольку прямая MN параллельна стороне AC, углы BMN и BAC равны как соответственные при параллельных прямых AC и MN и секущей BA. Следовательно, треугольники ABC и MBN подобны по двум углам.
Значит, BC / BN = AC / MN = 130 / 26 = 5, а поскольку BC / BN = ( BN + NC ) / BN = 1 + 56 / BN, получаем: BN = 56 / (5 - 1) = 56 / 4 = 14