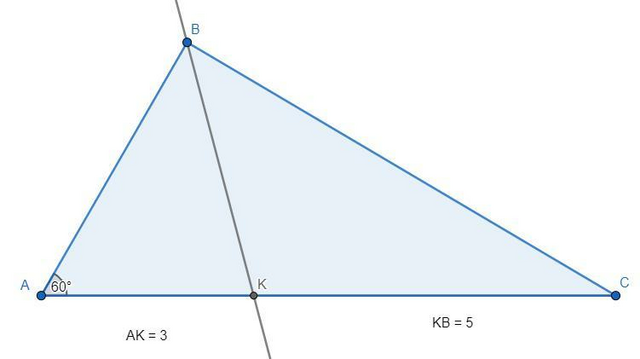
Из свойств биссектрисы:

Пусть AB=3x, тогда CB=5x
--------------------------
запишем теорему косинусов для треугольника ABC:

Значение косинуса, варьируется от (-1) до (1)
Значит при cos(BAC)=1 мы найдем минимальное значение x, а при cos(BAC)=(-1) максимальное.
-----------------
При cos(BAC)=1:

Так как нас интересуют только положительные значения x, остается только корень: x=1;
-----------------
При cos(BAC)=(-1):

Значит x варьируется от 1 до 4.
Значит периметр варьируется от:

Ответ Периметр изменяется от 16 см до 40 см