Помогите с геометрией пожалуйста. 50 баллов

Ответ:

Объяснение:

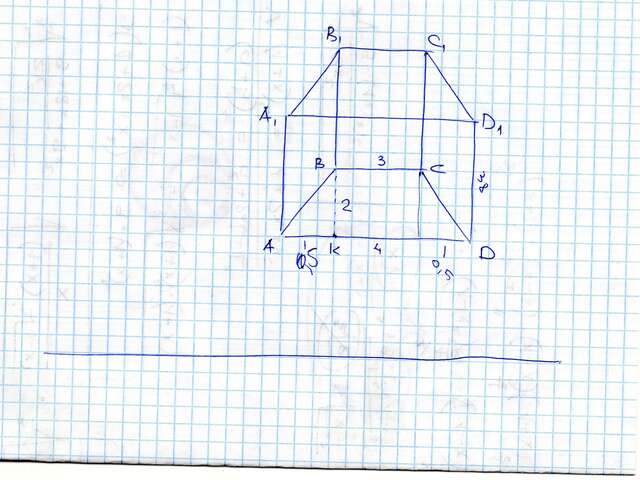
Площадь полной поверхности равна сумме площадей всех граней.

1. Площадь трапеции равна произведению ее средней линии на высоту

S ABCD = S A1B1C1D1 = $\frac{AD+BC}{2} BK$ = $\frac{4+3}{2} 2$ = 7 см²

2. Площади боковых граней, являющихся прямоугольниками

S AA1D1D = AA1*AD = 38*4 = 152 см²

S BB1C1C = BB1*BC = 38*3 = 114 см²

Далее вычислим длину боковой грани трапеции по теореме Пифагора

AB²=BK²+AK²

AB = $\sqrt{2^{2}+0.5^{2}}= \sqrt{4,25}$ =2.062 см

S AA1B1B = DD1C1 C= AA1 * AB = $38*\sqrt{4,25}$ = 78,356 см²

В результате, суммируя площади граней получаем:

S= 152*2+114*2+7*2+78.356*2= 702,712 см²

Помогите с геометрией пожалуйста. 50 баллов​