а) В четырехугольник можно вписать окружность, если суммы противолежащих сторон равны. Все стороны ромба равны, суммы противолежащих сторон равны - в любой ромб можно вписать окружность.
Центр вписанной окружности - пересечение биссектрис. Диагонали ромба являются биссектрисами его углов, центр вписанной окружности ромба - пересечения диагоналей (O).
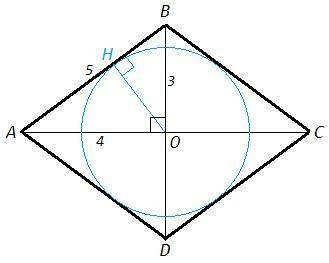
Диагонали ромба перпендикулярны, точкой пересечения делятся пополам. Треугольник ABO - египетский
AO=AC/2=4, BO=BD/2=3 => AB=5
OH - высота, проведенная из прямого угла
r= OH= AO*BO/AB =4*3/5 =2,4
(Расстояние от центра окружности до касательной - радиус.)
б) Около четырехугольника можно описать окружность, если сумма противолежащих углов равна 180. В ромбе противолежащие углы равны. Если их сумма 180, то углы прямые и ромб является квадратом. Данный ромб не является квадратом, так как его диагонали не равны. Следовательно около него нельзя описать окружность.
в) BCD - равнобедренный остроугольный. (BD=DC, стороны ромба. Данный ромб не является квадратом, угол BDC - острый.)
г) Синус угла в прямоугольном треугольнике - отношение противолежащего катета к гипотенузе.
В треугольнике ABO
sin(ABO)= AO/AB =4/5