Ответ:
Средняя линия: EF = 5,5√5 ед.
Площадь трапеции: Sabcd = 82,5 ед²
Объяснение:
Найдем длины (модули) отрезков:
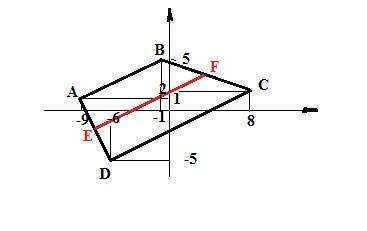
|АВ| = √((Xb-Xa)²+(Yb-Ya)²) = √((-1-(-9))²+(5-1)²) = √80 = 4√5 ед.
|BC| = √((Xc-Xb)²+(Yc-Yb)²) = √((8-(-1))²+(2-5)²) = √90 = 3√10 ед.
|CD| = √((Xd-Xc)²+(Yd-Yc)²) = √((-6-8))²+(-5-2)²) = √245 = 7√5 ед.
|АD| = √((Xd-Xa)²+(Yd-Ya)²) = √((-6-(-9))²+(-5-1)²) = √45 = 3√5 ед.
Два вектора коллинеарны (параллельны), если отношения их координат равны. В нашем случае это векторы
АВ{8;4} и CD{14;7}, так как 8/14 = 4/7. Следовательно, основания трапеции - это отрезки АВ и CD. Меньшая из боковых сторон - AD - высота прямоугольной трапеции.
Тогда имея длины всех сторон и определив, какие из них являются основаниями, найдем:
Среднюю линию: EF = (AB+CD)/2 = 11√5/2 = 5,5√5 ед.
Площадь трапеции: Sabcd = EF·AD = (5,5√5)·3√5 = 82,5 ед²
Или так:
Средняя линия трапеции - отрезок, соединяющий середины боковых сторон. Найдем координаты середин сторон АD и BC - точек E и F соответственно:
Е((Xa+Xd)/2; (Ya+Yd)/2) или Е((-9-6)/2; (1-5)/2).
F((Xb+Xc)/2; (Yb+Yc)/2) или F((-1+8)/2; (5+2)/2). Итак, имеем точки:
E(-7,5;-2) и F(3,5;3,5). Тогда длина средней линии равна:
|EF| = √((Xf-Xe)²+(Yf-Ye)²) = √((3,5-(-7,5))²+(3,5-(-2))²) = √151,25 ед.
Или EF = √151,25 = 5,5√5 ед.
Площадь трапеции равна средней линии, умноженной на высоту.
Sabcd = EF·AD = 5,5√5·3√5 = 3·27,5 = 82,5 ед².