Событие  — мишень поражена одним выстрелом. Рассмотрим следующие гипотезы:
— мишень поражена одним выстрелом. Рассмотрим следующие гипотезы:
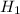 — мишень поражена только первым стрелком
— мишень поражена только первым стрелком
 — мишень поражена только вторым стрелком
— мишень поражена только вторым стрелком
 — мишень поражена только первым и вторым стрелками
— мишень поражена только первым и вторым стрелками
 — ни один стрелок не попал.
— ни один стрелок не попал.
Обозначим события  - попадание в мишень первым и вторым стрелками соответственно.
- попадание в мишень первым и вторым стрелками соответственно.

Условные вероятности:

По формуле Байеса, искомая вероятность:

Ответ: 4/7.