Основнания равнобокой трапеции равны 30дм и 40дм,а её боковая сторона 13дм. найдите...

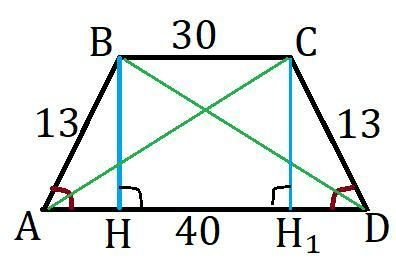
Смотри рисунок.

Диагонали равны т.к. углы при при основании и боковые стороны равнобокой трапеции равны (ΔABD=ΔACD). Из вершины B проведём высоты BH на сторону AD и высоту CH₁. BH=CH₁ как расстояние между параллельными прямыми, AB=CD как боковые стороны равнобокой трапеции и ∠CDH₁=∠BAH как углы при основании этой трапеции получается что ΔCDH₁=ΔBAH по катету, гипотенузе и углу. Таким образом AH=DH₁ как соответственные стороны равных треугольников.

BCH₁H это прямоугольник т.к. противоположные стороны параллельны и равны, а угол между ними 90°, то есть BC=HH₁. Найдём AH:

$\frac{AD-BC}{2} =AH\\AH=\frac{40-30}{2} =5$

$\cos{(BAH)}=\frac{AH}{BA} =\frac{5}{13}$ как угол я прямоугольном треугольнике. Тогда по теореме косинусов можно найти BD:

$BD^2=AB^2+AD^2-2AB*AD*\cos{(BAH)}\\BD^2=169+1600-400=1369=37^2\\BD=37$

Ответ: 37дм

Размерности были везде одинаковыми, поэтому можно было их и не писать.