1) Если функции монотонные, то сравнивать значения функции не трудно. Если функция возрастающая, то бОльшему значению аргумента соответствует бОльшее значение функции, то есть
если  x_2" alt="x_1>x_2" align="absmiddle" class="latex-formula"> , то
x_2" alt="x_1>x_2" align="absmiddle" class="latex-formula"> , то  f(x_2)" alt="f(x_1)>f(x_2)" align="absmiddle" class="latex-formula"> .
f(x_2)" alt="f(x_1)>f(x_2)" align="absmiddle" class="latex-formula"> .
Если функция убывающая, то бОльшему значению аргумента соответствует мЕньшее значение функции, то есть
если  x_2" alt="x_1>x_2" align="absmiddle" class="latex-formula"> , то
x_2" alt="x_1>x_2" align="absmiddle" class="latex-formula"> , то  .
.
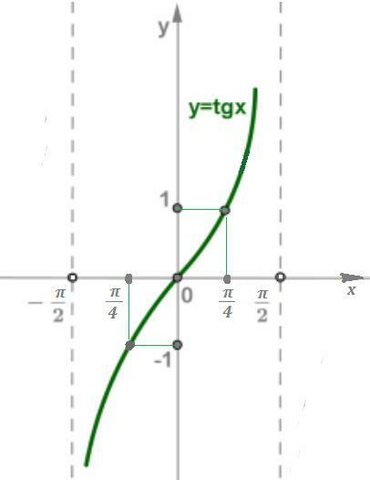
Функция y=tgx возрастающая при  . поэтому:
. поэтому:
 \frac{\pi}{8}\; \; \; \to \; \; \; tg\frac{\pi }{7}>tg\frac{\pi }{8}\\\\\frac{7\pi }{9}<\frac{8\pi}{9}\; \; \; \to \; \; \; tg\frac{7\pi }{9}<tg\frac{8\pi }{9}\\\\\frac{\pi}{11}\approx 0,285<\frac{13\pi }{12}\approx 3,402\; \; \; \to \; \; \; tg\frac{\pi }{11}<tg\frac{13\pi }{12}" alt="\frac{\pi}{7}>\frac{\pi}{8}\; \; \; \to \; \; \; tg\frac{\pi }{7}>tg\frac{\pi }{8}\\\\\frac{7\pi }{9}<\frac{8\pi}{9}\; \; \; \to \; \; \; tg\frac{7\pi }{9}<tg\frac{8\pi }{9}\\\\\frac{\pi}{11}\approx 0,285<\frac{13\pi }{12}\approx 3,402\; \; \; \to \; \; \; tg\frac{\pi }{11}<tg\frac{13\pi }{12}" align="absmiddle" class="latex-formula">
\frac{\pi}{8}\; \; \; \to \; \; \; tg\frac{\pi }{7}>tg\frac{\pi }{8}\\\\\frac{7\pi }{9}<\frac{8\pi}{9}\; \; \; \to \; \; \; tg\frac{7\pi }{9}<tg\frac{8\pi }{9}\\\\\frac{\pi}{11}\approx 0,285<\frac{13\pi }{12}\approx 3,402\; \; \; \to \; \; \; tg\frac{\pi }{11}<tg\frac{13\pi }{12}" alt="\frac{\pi}{7}>\frac{\pi}{8}\; \; \; \to \; \; \; tg\frac{\pi }{7}>tg\frac{\pi }{8}\\\\\frac{7\pi }{9}<\frac{8\pi}{9}\; \; \; \to \; \; \; tg\frac{7\pi }{9}<tg\frac{8\pi }{9}\\\\\frac{\pi}{11}\approx 0,285<\frac{13\pi }{12}\approx 3,402\; \; \; \to \; \; \; tg\frac{\pi }{11}<tg\frac{13\pi }{12}" align="absmiddle" class="latex-formula">
2)  .
.
Точку  отмечаем на расстоянии 3 клеточек ( 1,5 см ) от точки О , так как
отмечаем на расстоянии 3 клеточек ( 1,5 см ) от точки О , так как  см = 6 клеточкам ,
см = 6 клеточкам ,  см. Смотри рисунок.
см. Смотри рисунок.