D(x) € R, кроме x = -1
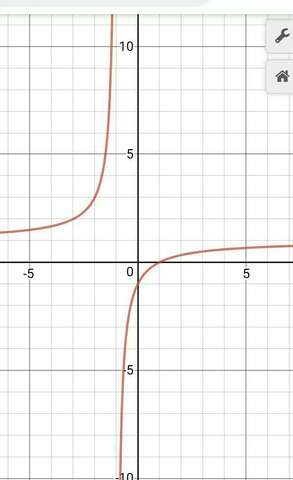
следовательно, х= -1 точка разрыва и вертикальная асимптота.
определим четность или нечестность.
у(-х) =(-х-1) / (-х+1) => функция и не четная, и не нечетная
найдем нули функции.
х=0, y=-1
y=0, x=1.
Производная

видно, что производная для все х больше нуля, следовательно, сама функция не имеет критических точек, и неизменно возрастает на всем определенном х.
иследуем поведение функции в точке разрыва и на бесконечности.
при х стремящимся к (+-) бесконечности, у стремится 1.
при х стремящимся к -1 слева, у стремится к бесконечности
при х стремящимся к -1 справа, у стремится к минус бесконечности
осталось построить