0≤α≤2π
ρ≥0
У cos(x) для х периодичность 2π, то есть у cos(3α) для 3α периодичность 2π --> для α периодичность 2π/3.
У косинуса область значение не больше 1 --> область значений функции p не больше 1*2=2. Начертим окружность с радиусом 2 и центром (0;0), все значения функции будут лежать на окружности или внутри неё.
Разобьём окружность на три сектора по 2π/3, в них значение функции будет одинаковым (длина вектора или p).
2cos(3α)=2 --> α=0+2πk/3, k∈Z
2cos(3α)=0 --> α=π/6+2πk/3, k∈Z
На этом промежутке функция убывает.
2cos(3α)∈(0;-2) --> α∈(π/6+2πk/3;π/2+2πk/3), k∈Z
При этом p≥0, то есть в последнем промежутке функция не определена.
α∈[π/2+2πk/3;2π/3+2πk/3], k∈Z --> 2cos(3α)∈[0;2]
На этом промежутке функция растёт.
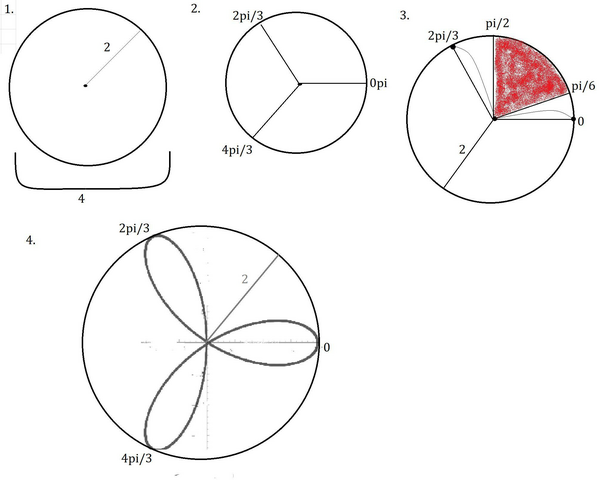
Изобразим то, что получилось.
Осталось только скопировать и перенести эти фрагменты, предварительно не забыв развернуть на соответственный угол (2π/3), т.к. на плоскости координаты точки зависят не только от длины вектора, но и от угла наклона. А периодична именно функция, то есть длина вектора, в то время как угол всегда разный.