Сколько ришений имеет система 1){у=х^2-1 {х+у=4 2) {х^2+у^2=9 {х-у=5 Срочно пожалуйста у...

$\left \{ {{y=x^2-1} \atop {y=4-x}} \right.$

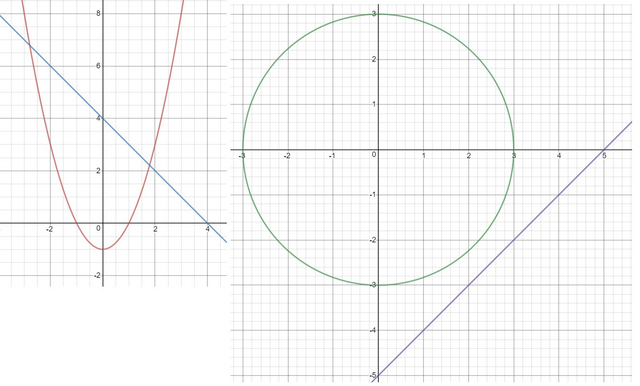
Вершина параболы (0;-1), ветви направлены вверх. точки пересечения в осями:

$y(0)=0^2-1=-1\\x(0)=б1$

Вторая функция, это прямая образующая с осью х угол 135° и она пересекает оси в точках:

$y(0)=4-0=4\\x(0):4$

Построив график можно увидеть, что у системы всего 2 решения. Вроде самая точки находить не надо.

$\left \{ {{x^2+y^2=3^2} \atop {y=x-5}} \right.$

Первая функция это уравнение окружности с центром в точке (0;0) и радиусом 3.

Вторая функция, это прямая образующая угол 45° с осью х, и пересекает оси в точках:

$y(0)=0-5=-5\\x(0)=5$

Построив график можно увидеть, что система не имеет решений.