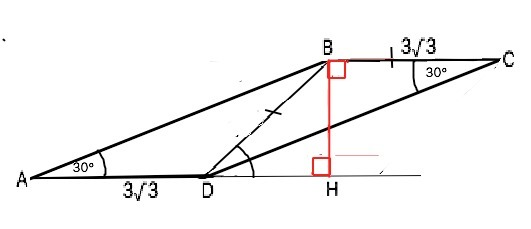
В параллелограмме противоположные углы равны. ⇒ угол ВСD=30°. По условию ВD=ВС, следовательно, углы при основании DC равнобедренного треугольника ВСD равны. Поэтому ∠DBC=180°-2•30°=120°. Диагональ параллелограмма делит его на два равных треугольника. Следовательно, Ѕ(АВСD)=2•Ѕ(ВСD). Одна из формул площади треугольника S=a•b•sinα:2, где а и b - соседние стороны треугольника, α - угол между ними. Ѕ(АВСD)=2•(BC•BD•sin120°):2=(3√3)²•√3/2=27√3/2 см²
———
Вариант решения. Угол BDC=30°, угол СDH=углу ВСD=30° (накрестлежащие) ⇒ угол ВDH=60°⇒ BH=BD•sin60°=3√3•√3/2=9/2. ⇒ S(ABCD)=AD•BH=3√3•9/2=27√3/2