1) ΔАВС , ∠С=90° , ∠А=38° , с=АВ=12 см .
∠В=90°-38°=52°
sin∠A=CB/АВ=CB/12 ⇒ CB=12·sin38°≈12·0,62=7,44
sin∠B=AC/AB=AC/12 ⇒ AC=12·sin52°≈12·0,79=9,48
2) ΔАВС , ∠С=90° , АC/ВС=5/2 ⇒ АС=5х , ВС=2х ⇒
tg∠A=2x/5x=2/5=0,4 ⇒ ∠A=arctg0,4≈22°
tg∠B=5x/2x=5/2=2,5 ⇒ ∠B=arctg2,5≈68° ( или ∠В=90°-22°=68° )
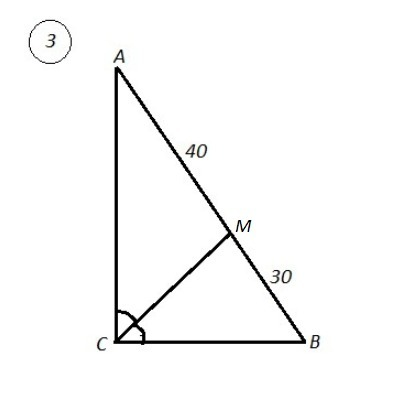
3) ΔАВС , ∠С=90° , СМ - биссектриса , АМ=40 дм , ВМ=30 дм .
СМ - биссектриса ⇒ АМ/АС=ВМ/ВС ⇒ АМ/ВМ=АС/ВС , 40/30=АС/ВС
АС/ВС=4/3 ⇒ АС=4х , ВС=3х ,
АВ=√(АС²+ВС²)=√((4х)²+(3х)²)=√25х²=5х ,
АВ=АМ+ВМ=40+30=70 ⇒ 5х=70 ,
х=70:5=14 (см)
АС=4х=4·14=56 (см) , ВС=3·14=42 (см) ,
Периметр Р=АС+ВС+АВ=56+42+70=168 см .