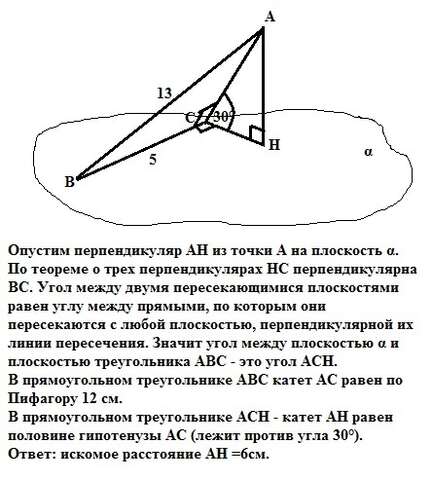
Опустим перпендикуляр АН из точки А на плоскость α. По теореме о трех перпендикулярах НС перпендикулярна ВС. Угол между двумя пересекающимися плоскостями равен углу между прямыми, по которым они пересекаются с любой плоскостью, перпендикулярной их линии пересечения. Значит угол между плоскостью α и плоскостью треугольника АВС - это угол АСН.
В прямоугольном треугольнике АВС катет АС равен по Пифагору 12 см.
В прямоугольном треугольнике АСН - катет АН равен половине гипотенузы АС (лежит против угла 30°) = 6см..
Ответ: искомое расстояние АН =6см.