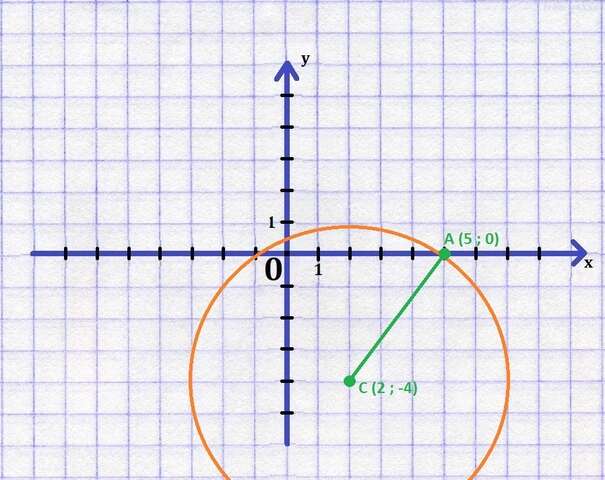
Найти уравнение окружности.
Общая формула окружности:  где (a; b) - центр окружности, R - её радиус.
где (a; b) - центр окружности, R - её радиус.
Центр нам уже известен. Половина задачи решена!
Найдём радиус окружности.
Радиус равен расстоянию между данной точкой A и центром C.
Формула: 

Подставляем полученное в общую формулу окружности.
Получаем: 
График можно увидеть в приложении.
Ответ: (x - 2)² + (y + 4)² = 25.