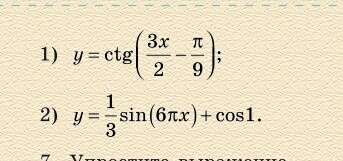Очень нужно решение этих заданий, пожалуйста. Если можно, то подробно) 1. Найдите...

0 голосов
49 просмотров

Очень нужно решение этих заданий, пожалуйста. Если можно, то подробно) 1. Найдите множество значений функции: y=2cos3x + 1 2. Найдите наименьший положительный период функции: 1) y=ctg (3x/2-п/9) 2) у= 1/3sin(6пх)+соs1 Учитель Очень придирчивый, Если 2 задание не совсем понятно, прикрепила фото, где эти функции хорошо видны. ЗАРАНЕЕ БОЛЬШОЕ СПАСИБО❤

image
Алгебра (59 баллов) | 49 просмотров
0

А какое множество значений будет у функции y=cosx?

оставил комментарий (4.4k баллов)
0

Вроде от -1 до 1

оставил комментарий (59 баллов)
0

А как они изменяться если отнять от них 1 и разделить потом на 2?

оставил комментарий (4.4k баллов)
0

Почему отнять и разделить?

оставил комментарий (59 баллов)
0

ну ведь у вас же в 1 задание не просто y=cosx

оставил комментарий (4.4k баллов)
0

Да, но мне казалось, что нужно прибавить и умножить... Или я совсем что-то не так понимаю, но не уверена в своих знаниях

оставил комментарий (59 баллов)
0

как из функции cosx сделать вашу, нужно умножить её на 2, а затем прибавить 1, эти же самые операция вы проводите над -1 и 1

оставил комментарий (4.4k баллов)
0

умножение в косинусе никак не изменяют область значений, поэтому что cos3x что cosx область значений будет та же

оставил комментарий (4.4k баллов)
Дан 1 ответ
0 голосов

Решите задачу:

1) y=cosx=[-1;1]\\ \\ -1\leq 2cos3x+1\leq 1\\ \\ -1\leq cos3x \leq1\\ -2\leq 2cos3x \leq2\\ -1\leq 2cos3x+1 \leq3\\ \\ E(x)=[-1;3]\\ \\ \\ 2)T_0(ctg)=\pi\\ \\ T_0=\pi:\frac{3}{2} =\frac{2\pi}{3} \\ \\ T_0(sin)=2\pi\\ \\ T_0=\frac{2\pi}{6\pi} =\frac{1}{3}

(10.7k баллов)
0

+1 забыли в области значений функции справа

оставил комментарий (4.4k баллов)
Похожие задачи