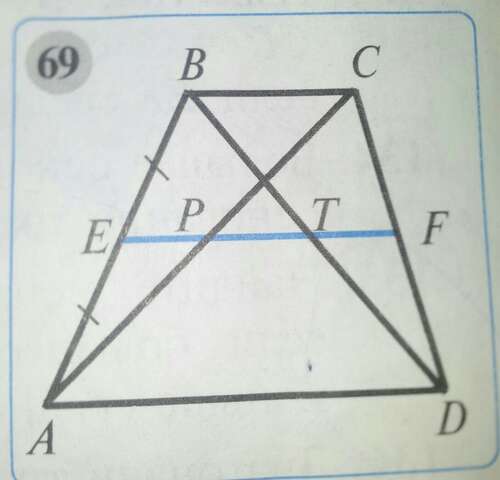
Диагонали трапеции делят её среднюю линию на отрезки, длины которых равны 5см, 4см, и 7 см. Найдите длины оснований трапеции (см. рис. 69). Заполните пропуски. Решение. В треугольнике ABC отрезок EP является.... Следовательно, BC=…см ( по свойству...). В треугольнике ACD отрезок PF является... . PF=…+…=…см+…см=…см. Поэтому AD=…см. Ответ :….