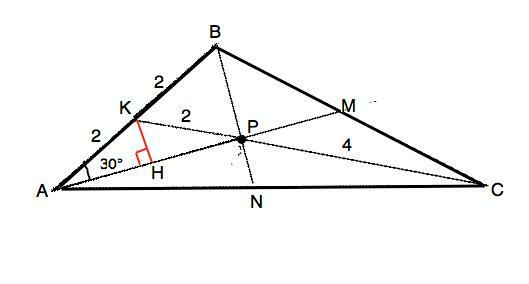
Ответ: РМ=√3
Объяснение:
Медианы треугольника пересекаются в одной точке. Следовательно, отрезок СР - часть медианы из С, Продолжим ее до пересечения с АВ в точке К.
Медианы треугольника точкой пересечения делятся в отношении 2:1, считая от вершины. ⇒ РК=СР:2=4:2=2.
Точка К - середина АВ. ⇒
АК=КВ=2.
Треугольник АКР равнобедренный ( АК=КР).
Из К опустим высоту КН на АР. Отрезок КН=АК:2=1 (свойство катета, противолежащего углу 30°).
Тогда АН=НР=КН•ctg30°=√3 ⇒ АР=2√3
По свойству медиан АР:РМ=2:1, поэтому РМ=0.5•2√3=√3