Показать штриховкой ** координатной плоскости множество точек, заданное системой...

Question

Дано ответов: 2

Правильный ответ

$\left \{ {{y\leq x^2+2} \atop {y<7\; \; \; \; }} \right.$

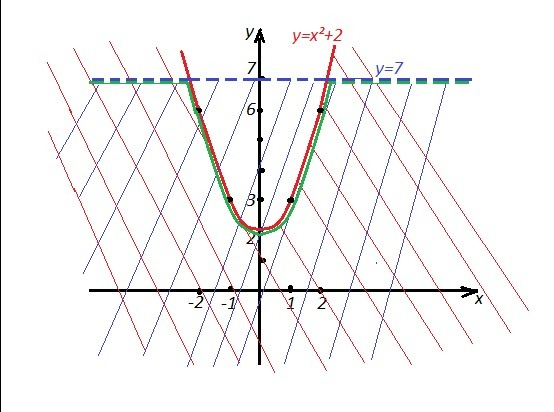
Нарисуем параболу у=х²+2, ветви вверх, вершина в точке (0,2) . Надо заштриховать область, расположенную ниже этой параболы.

Нарисуем прямую у=7, она проходит параллельно оси ОХ через точку (0,7) . Надо заштриховать область, расположенную ниже этой прямой. Так как неравенство у<7 строгое, то линия у=7 не входит в область, её рисуем штриховой линией.</p>

Тогда область, соответствующая системе неравенств, будет та, которая получается в результате наложения штриховок. Верхняя граница этой области обведена зелёной линией.

NNNLLL54_zn (834k баллов) 20 Май, 20

AntVa_zn · Answer 1 · 2020-05-20T08:21:42+0000

$\left \{ {{y}\leq x^{2}+2; \atop {y\textless7;}} \right.$

первое неравенство это синий и красный - парабола ветви вверх, зеленый и красный это линия. Нужный диапазон это пересечение синего и зеленного превратившийся в красный цвет(зелень+синева).

По поводу строгого и не строгого неравенства. Второе уравнение зеленная линия не включает саму себя как линию, y<7;</p>

А вот первое уравнение включает линию самой параболы синего цвета.

Красный цвет это и есть штриховка на координатной плоскости.