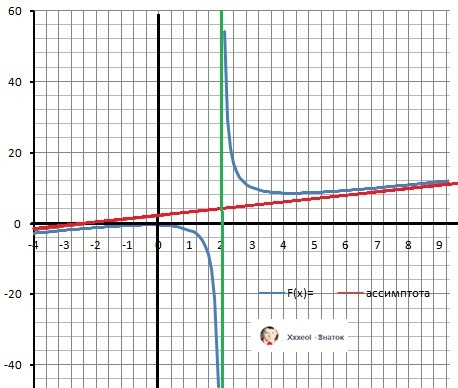
График к задаче на рисунке в приложении.
ДАНО Y=(x²1)/(x-2)
ИССЛЕДОВАНИЕ
1. Область определения.
x-2 ≠ 0, Х≠ .
Х∈(-∞;2)∪(2;+∞)
2. Вертикальная асимптота: Х= 2.
3. Пересечение с осью Х.
x² +1 = 0. x1 = -1
4. Пересечение с осью У.
Y(0) = (0²+1)/(0-2) = -1/2.
5. Наклонная асимптота.
k = lim(Y(x)/x)
Уравнение асимптоты: Y = x +2.
6. Проверка на чётность.
Y(-x) ≠ Y(x). Y(-x) ≠ - Y(x)
Функция ни четная ни нечетная.
7. Поведение в точке разрыва.
lim(->2-) Y(x) = -∞.
lim(->2+) Y(x) = +∞
8, Первая производная.

6. Локальные экстремумы
x1 = 2-√5 (≈0.24) , x2 = 2+√5 (≈4.24)
Максимум - ? . Минимум - ?.
7. Участки монотонности функции.
Возрастает Х∈(-∞;x1)∪[(x2;+∞).
8. Вторая производная
Точка перегиба - х = 2.
9. Выпуклая - "горка" - Х∈(-∞;2)
Вогнутая - "ложка" - Х∈(2;+∞)