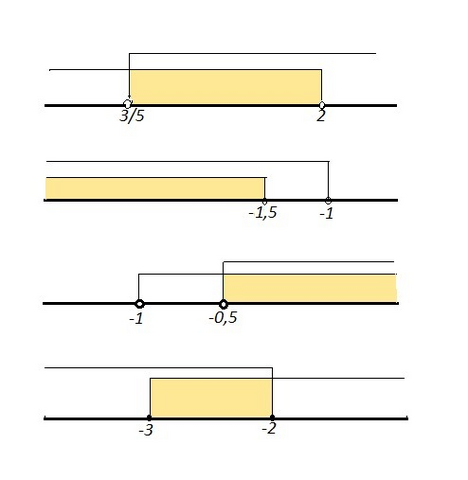
0} \atop {5x-3>0}} \right. \; \left \{ {{3x<6} \atop {5x>3}} \right. \; \left \{ {{x<2} \atop {x>\frac{3}{5}}} \right. \; \; \Rightarrow \; \; \frac{3}{5}10}} \right. \; \left \{ {{4x<-4} \atop {2x<-3}} \right. \; \left \{ {{x<-1} \atop {x<-1,5}} \right. \; \; \Rightarrow \; \; x<-1,5\\\\x\in (-\infty ,-1,5)" alt="712)\; \; \left \{ {{6-3x>0} \atop {5x-3>0}} \right. \; \left \{ {{3x<6} \atop {5x>3}} \right. \; \left \{ {{x<2} \atop {x>\frac{3}{5}}} \right. \; \; \Rightarrow \; \; \frac{3}{5}10}} \right. \; \left \{ {{4x<-4} \atop {2x<-3}} \right. \; \left \{ {{x<-1} \atop {x<-1,5}} \right. \; \; \Rightarrow \; \; x<-1,5\\\\x\in (-\infty ,-1,5)" align="absmiddle" class="latex-formula">
0} \atop {5x-3>0}} \right. \; \left \{ {{3x<6} \atop {5x>3}} \right. \; \left \{ {{x<2} \atop {x>\frac{3}{5}}} \right. \; \; \Rightarrow \; \; \frac{3}{5}10}} \right. \; \left \{ {{4x<-4} \atop {2x<-3}} \right. \; \left \{ {{x<-1} \atop {x<-1,5}} \right. \; \; \Rightarrow \; \; x<-1,5\\\\x\in (-\infty ,-1,5)" alt="712)\; \; \left \{ {{6-3x>0} \atop {5x-3>0}} \right. \; \left \{ {{3x<6} \atop {5x>3}} \right. \; \left \{ {{x<2} \atop {x>\frac{3}{5}}} \right. \; \; \Rightarrow \; \; \frac{3}{5}10}} \right. \; \left \{ {{4x<-4} \atop {2x<-3}} \right. \; \left \{ {{x<-1} \atop {x<-1,5}} \right. \; \; \Rightarrow \; \; x<-1,5\\\\x\in (-\infty ,-1,5)" align="absmiddle" class="latex-formula">
 x+3}} \right. \; \left \{ {{-1-2<7x-x} \atop {11x-x>3-13}} \right. \; \left \{ {{6x>-3} \atop {10x>-10}} \right. \; \left \{ {{x>-0,5} \atop {x>-1}} \right. \; \Rightarrow x>-0,5\\\\x\in (-0,5\, ;+\infty )\\\\725)\; \; \left \{ {{x-1\leq 2x+2} \atop {3x+5\leq x+1}} \right. \; \left \{ {{-3\leq x} \atop {2x\leq -4}} \right. \; \left \{ {{x\geq -3} \atop {x\leq -2}} \right. \; \; \Rightarrow \; \; -3\leq x\leq -2\\\\x\in [-3,-2\, ]" alt="721)\; \; \left \{ {{x-1<7x+2} \atop {11x+13>x+3}} \right. \; \left \{ {{-1-2<7x-x} \atop {11x-x>3-13}} \right. \; \left \{ {{6x>-3} \atop {10x>-10}} \right. \; \left \{ {{x>-0,5} \atop {x>-1}} \right. \; \Rightarrow x>-0,5\\\\x\in (-0,5\, ;+\infty )\\\\725)\; \; \left \{ {{x-1\leq 2x+2} \atop {3x+5\leq x+1}} \right. \; \left \{ {{-3\leq x} \atop {2x\leq -4}} \right. \; \left \{ {{x\geq -3} \atop {x\leq -2}} \right. \; \; \Rightarrow \; \; -3\leq x\leq -2\\\\x\in [-3,-2\, ]" align="absmiddle" class="latex-formula">
x+3}} \right. \; \left \{ {{-1-2<7x-x} \atop {11x-x>3-13}} \right. \; \left \{ {{6x>-3} \atop {10x>-10}} \right. \; \left \{ {{x>-0,5} \atop {x>-1}} \right. \; \Rightarrow x>-0,5\\\\x\in (-0,5\, ;+\infty )\\\\725)\; \; \left \{ {{x-1\leq 2x+2} \atop {3x+5\leq x+1}} \right. \; \left \{ {{-3\leq x} \atop {2x\leq -4}} \right. \; \left \{ {{x\geq -3} \atop {x\leq -2}} \right. \; \; \Rightarrow \; \; -3\leq x\leq -2\\\\x\in [-3,-2\, ]" alt="721)\; \; \left \{ {{x-1<7x+2} \atop {11x+13>x+3}} \right. \; \left \{ {{-1-2<7x-x} \atop {11x-x>3-13}} \right. \; \left \{ {{6x>-3} \atop {10x>-10}} \right. \; \left \{ {{x>-0,5} \atop {x>-1}} \right. \; \Rightarrow x>-0,5\\\\x\in (-0,5\, ;+\infty )\\\\725)\; \; \left \{ {{x-1\leq 2x+2} \atop {3x+5\leq x+1}} \right. \; \left \{ {{-3\leq x} \atop {2x\leq -4}} \right. \; \left \{ {{x\geq -3} \atop {x\leq -2}} \right. \; \; \Rightarrow \; \; -3\leq x\leq -2\\\\x\in [-3,-2\, ]" align="absmiddle" class="latex-formula">