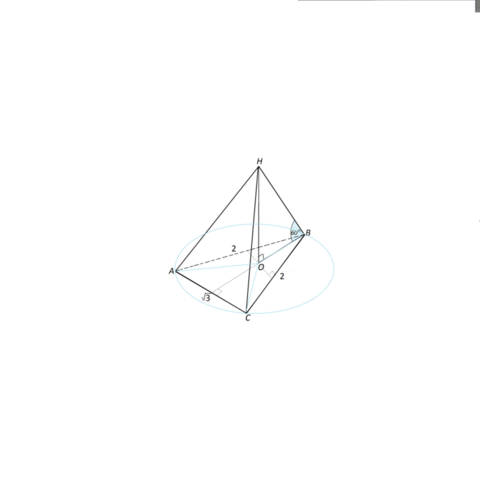
Объем пирамиды находят по формуле
V=Sh:3
Площадь S основания найдем по формуле площади равнобедренного треугольника через его стороны 2,√3,2.
S=0,25b√(4a²-b²), где а - боковая сторона, b- основание треугольника.
S=0,25√3√(16-3)=0,25*√3√13 см²
(Можно и по классической формуле =ah:2, но это будет немного дольше - надо находить высоту треугольника)
Высоту НО пирамиды найдем из треугольника, образованного ее ребром
НВ- гипотенуза, и катетами - расстояние ОВ от основания высоты до вершин треугольника и высота НО, с углом НВО=60°.
Расстояние от основания высоты до вершин треугольника - это радиус описанной вокруг треугольника окружности, так как все ребра наклонены к основанию пирамиды под углом 60°, и на этом основании их проекции равны этому радиусу.
Радиус описанной окружности найдем по формуле для радиуса окружности, описанной вокруг равнобедренного треугольника.
R=a²:√(4a²-b²)R=4:√(16-3)=4:√13 см
НО=R:Ctg(60°) = (4:√13):1/√3=(4√3):√13 см
V=Sh:3
V=(0,25*√3√13)(4√3):√13):3=1 см³