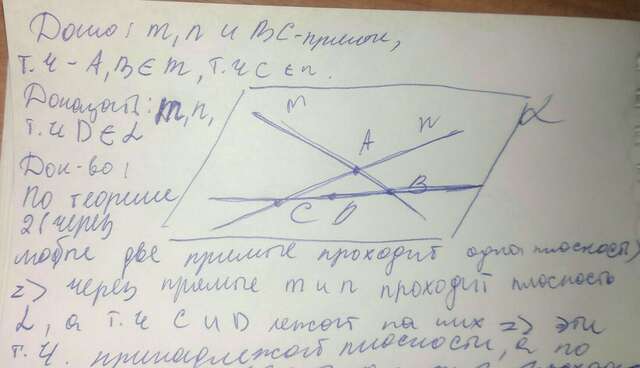
Дано: m, n, BC-прямые, т.ч. А, В принадлежат прямой m, т.ч С принадлежит прямой n.
Доказать: m,n и т.ч. D принадлежит плоскости L (альфа)
Доказательство:
По теореме 2 (Через две пересекаемые прямые проходит плоскость, и притом только одна), следовательно через прямые m, n проходит плоскость L, а точки С и В принадлежат этим прямым, плоскости и лежат на прямой ВС, а по аксиоме 2 (Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости), следовательно прямая ВС, тоже принадлежит плоскости, а т.ч D принадлежит прямой ВС, значит т.ч. тоже лежит в плоскости. Доказано.