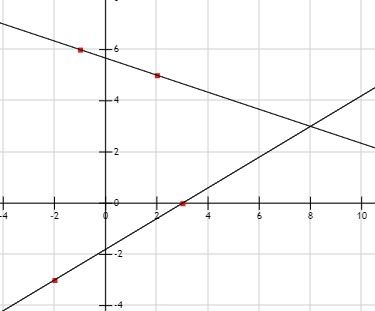
Уравнение прямой, проходящей через 2 точки
(y₁ - y₂)x + (x₂ - x₁) + (x₁y₂ - x₂y₁) = 0
через точки M(-1;6), N(2;5)
x+3y−17=0
через точки k(3;0) e(-2;-3)
3x−5y−9=0
Точка пересечения прямых MN и ke принадлежит каждой из пересекающихся прямых MN и ke. Следовательно, координаты точки пересечения прямых MN и ke удовлетворяют одновременно и уравнению x+3y−17=0 и уравнению 3x−5y−9=0. Значит, координаты точки пересечения двух прямых MN и ke являются решением системы уравнений:

x=17-3y
3(17-3y)-5y-9 = 0
51-9y-5y-9 = 0
-14y = -42
y=3
x=17-9 = 8
Ответ: Точка пересечения прямых MN и ke (8;3).