Как построить график функции y=-x^2-5x+6(квадратичная) помогите пожалуйста!!!!

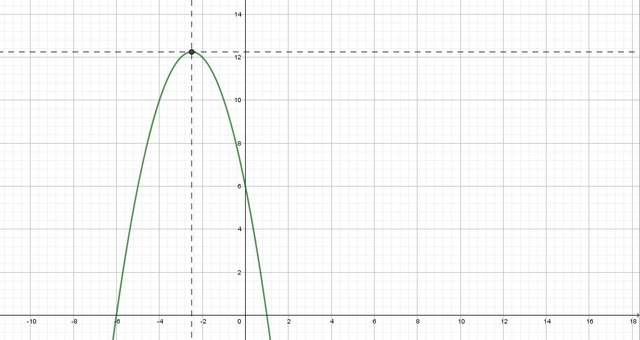
Графиком квадратичной функции является парабола, ветви которой направлены вниз, так как a = -1 < 0. Найдем координаты вершины параболы

$x=-\dfrac{b}{2a} =\dfrac{5}{2\cdot(-1)} =-2.5$

Значение абсциссы вершины параболы подставить в функцию:

$y=-(-2.5)^2-5\cdot(-2.5)+6=-6.25+12.5+6=12.25$

Таким образом, получили точку A вершины параболы, координаты которой (-2.5; 12.25).