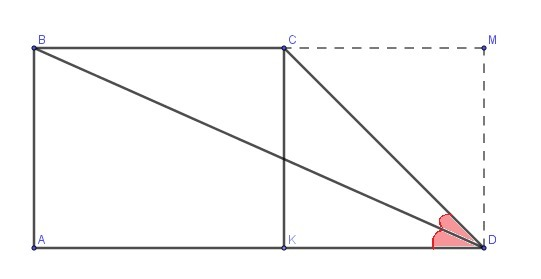
BD - більша діагональ, бісектриса кута 60°, тобто діагональ BD ділить кут D навпіл: 
З прямокутного трикутника BAD знайдемо основу АD
 см.
см.
Розглянемо прямокутний трикутник CKD:  см
см
Із точки D проведемо перпендикуляр DM на проводженні сторони BC, маємо, що площа прямокутного трикутника CMD:  см², а площа прямокутника ABMD:
см², а площа прямокутника ABMD:  см²
см²
Остаточно маємо:  см²
см²
Ответ: 120√3 см².