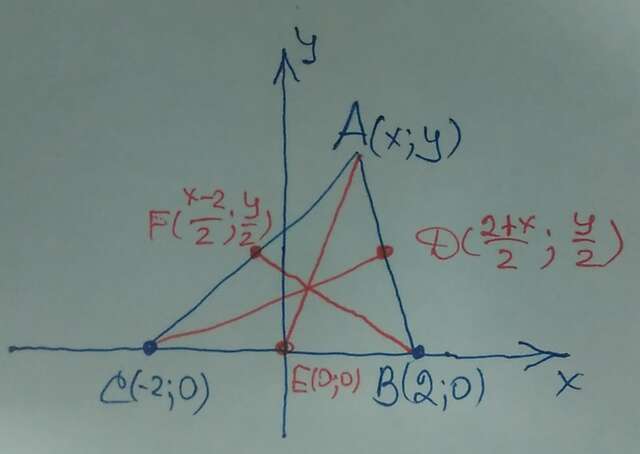
Тупоугольный треугольник АВС
Угол А тупой
Сторона ВС = 4
Медианы АЕ, BF, CD
Координаты вершин
A(x;y)
B(2;0)
C(-2;0)
D((2+x)/2;y/2)
E(0;0)
F((x-2)/2;y/2)
Тупоугольным треугольник будет только если вершина А лежит внутри окружности, построенной на стороне CD и диаметром 4
AE² = x² + y² < 2²
|AE| < 2
Медиана АЕ меньше 2
Медиана ВF
ВF² = (2 – (x-2)/2)² + y²/4 = 1/4*(x² – 12x + y² + 36)
Медиана СD
CD² = ((2+x)/2+2)² + y²/4 = 1/4*(x² + 12x + y² + 36)
Сумма медиан CD и BF
S(x;y) = 1/2*sqrt(x² – 12x + y² + 36) + 1/2*sqrt(x² + 12x + y² + 36)
Производная по x, ищем экстремум
dS/dx = 1/4*((2(x - 6))/sqrt(x² - 12x + y² + 36) + (2(x + 6))/sqrt(x² + 12x + y² + 36)) = 0
(x - 6)/sqrt(x² - 12x + y² + 36) + (x + 6)/sqrt(x² + 12x + y² + 36) = 0
Числитель
(x - 6)*sqrt(x² + 12x + y² + 36) + (x + 6)*sqrt(x² - 12x + y² + 36) = 0
Тривиальное решение
х = 0 для любого y
Знаменатель при этом неважен, лишь бы оставался ненулевым
Это экстремум, но минимум или максимум — пока неизвестно.
Для определения проще всего вычислить значение S(0;2) и S(1;2)
S(0;2) = 1/2*sqrt(4 + 36) + 1/2*sqrt(4 + 36) = sqrt(40) ≈ 6,325
S(1;2) = 1/2*sqrt(1 – 12 + 4 + 36) + 1/2*sqrt(1 + 12 + 4 + 36) = 1/2*sqrt(29) + 1/2*sqrt(53) ≈ 6,333
Т.е. при x = 0 имеется минимум суммы длин медиан
Минимальной суммой медиан к боковым сторонам обладает равнобедренный треугольник
Производную по y можно не брать, т. к. по y сумма длин — функция возрастающая и максимальное значение суммы длин будет при максимальном значении y
Но из условия тупоугольности треугольника у нас y не может превосходить 2
Медиана к основанию тоже не превосходит 2, поэтому значение сумм длин всех трёх медиан будет не превосходить
S(0;2) + 2 = 2 + sqrt(40) ≈ 8,325
Что меньше требуемых по условию 9