ОДЗ: (как оказалось, не понадобится, но пусть будет)

Перемножаем крест на крест

При b=-1 получаем равенство 0=0, что дает бесконечно много решений на промежутке [π/4; π/2]

Делим на cosx

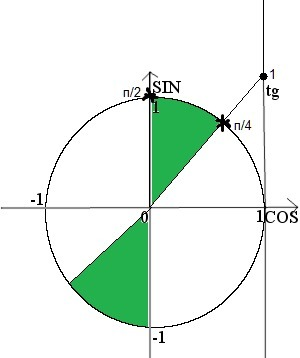
При помощи единичной окружности (прикрепил картинку), находим необходимые для выполнения условий значения b+1
Получили b+1∈[1; +∞) ⇒ b∈[0; +∞)
Ответ: b∈{-1}U[0; +∞)