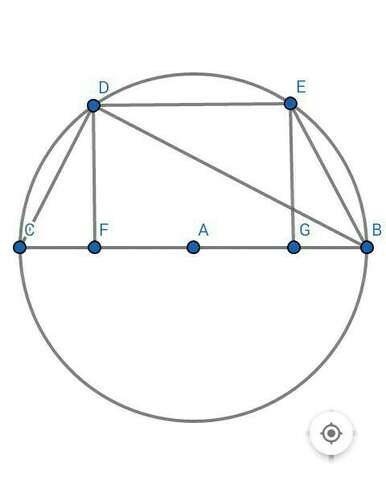
1) R = AB = AC = 10 cm
BC = 2R = 2 × 10 = 20 cm
2) Рассмотрим ∆ BCD ( угол BDC = 90° ) :
По теореме Пифагора :
BD² = BC² - BD²
BD² = 20² - 12² = 400 - 144 = 256 =
BD = 16 cm
DF - высота трапеции
S bcd = 1/2 × BD × CD
S bcd = 1/2 × DF × BC
Приравняем площади и получаем:
ВD × CD = DF × BC
DF = BD × CD / BC = 16 × 12 / 20 = 9,6 cm
3) Рассмотрим ∆ СDF ( угол CFD = 90° ) :
По теореме Пифагора :
CF² = CD² - DF²
CF² = 12² - 9,6² = 144 - 92,16 = 51,84
CF = BG = 7,2 cm
FG = DE = 20 - 7,2 - 7,2 = 5,6
S bcde = 1/2 × ( DE + BC ) × DF = 1/2 × ( 5,6 + 20 ) × 9,6 = 1/2 × 25,6 × 9,6 = 122,88 см²
ОТВЕТ: 122,88 см²