Формула выглядит по-другому. Вот доказательство.
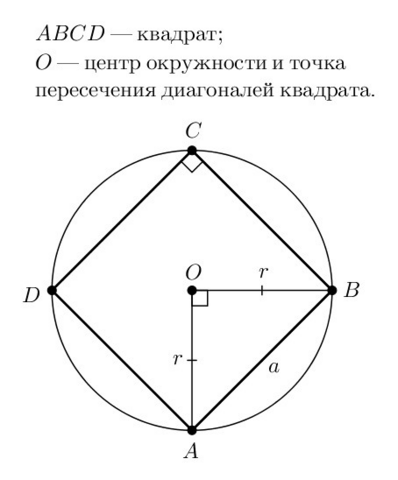
Диагонали квадрата равны, а также в точке пересечения делятся пополам. Следовательно, точка их пересечения O (см. обозначения на рисунке) равноудалена от всех вершин и поэтому является центром описанной окружности. Отрезки OA=OB=r — её радиусы. Рассмотрим Δ AOB. Диагонали квадрата, как и любого ромба, перпендикулярны, поэтому ∠AOB = 90°, а значит, Δ AOB — прямоугольный.
Теперь найдём сторону a по теореме Пифагора: