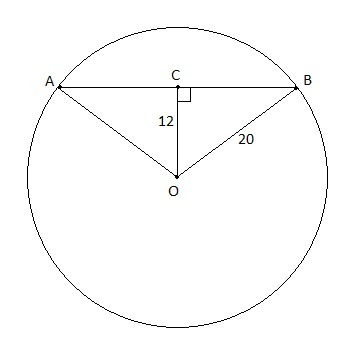
△AOB – равнобедренный, т.к
OA = OB = r; ⟹ OC – высота, медиана и
биссектриса; ⟹ AC = CB, а ∠OCB – прямой.
По теореме Пифагора: AC = √(OB² – OC²) = √(20² – 12²) =√256 = 16
AB
= 16 * 2 = 32
Или:
△AOB – равнобедренный, т.к OA = OB =
r; ⟹ OC – высота, медиана
и биссектриса; ⟹ ∠AOC = ∠COB = 1/2∠AOB, а ∠OCB –
прямой.
AB = 2r *
sin(∠AOB/2);
cos∠COB = OC/OB = 12/20 = 0,6;
sin∠COB = √(1 – cos∠COB²) = √(1 – 0,36) = √0,64 = 0,8;
AB = 2 * 20
* 0,8 = 32.