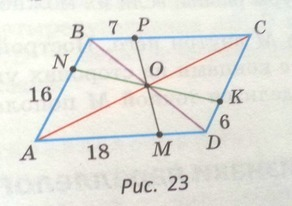
См. рис.1
Так как ABCD - параллелограмм, то: AO = OC; BO = OD.
По теореме о свойствах отрезков прямой, проходящей через точку пересечения диагоналей параллелограмма: OP = OM и OK = ON.
Так как ∠BOP = ∠MOD и ∠BON = ∠KOD, как вертикальные, то:
ΔВОР = ΔMOD по 1-му признаку равенства треугольников (по двум сторонам и углу между ними), то BP = MD = 7 см.
ΔBON = ΔDOK по тому же 1-му признаку равенства треугольников. Следовательно: BN = KD = 6 см.
Периметр параллелограмма АВСD:
Р = 2*(AB + AD) = 2*(16+6 + 18+7) = 2 * 47 = 94 (см)
-------------------------------
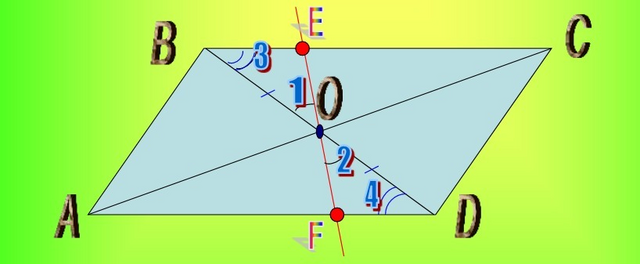
См. рис.2
Теорема о свойствах отрезков прямой, проходящей через точку пересечения диагоналей параллелограмма: Данные отрезки делятся точкой пересечения диагоналей параллелограмма пополам.
Доказательство: пусть АВСD - данный параллелограмм и EF - прямая, пересекающая параллельные стороны AD и ВС. Треугольники ВОЕ и FOD равны по второму признаку (стороне и двум прилежащим углам). В этих треугольниках:
ВО = ОD, так как О - середина диагонали АС,
Углы при вершине О равны, как вертикальные, а углы BOE и FOD равны, как внутренние накрест лежащие при параллельных АС и ВС и секущей BD. Из равенства треугольников следует равенство сторон: OE = OF, что и требовалось доказать.