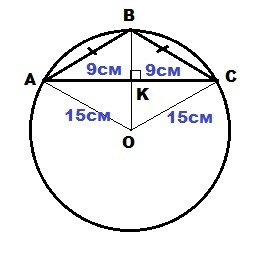
ΔABC - тупоугольный равнобедренный, AC=18 см; AB=BC
BK - высота и медиана: BK⊥AC; AK = KC = AC/2 = 18/2 = 9 см
ΔOKC - прямоугольный: ∠OKC = 90°. Теорема Пифагора
OK² = OC² - KC² = 15² - 9² = 144 = 12² ⇒ OK = 12 см
KB = OB - OK = 15 - 12 = 3 см
ΔBKC - прямоугольный: ∠BKC = 90°. Теорема Пифагора
BC² = KB² + KC² = 3² + 9² = 90 ⇒ BC = √90 = 3√10 см
Периметр ΔABC
P = AC + 2 BC = 18 + 6√10 см