1) Так как центр описанной окружности лежит на пересечении серединных перпендикуляров к сторонам треугольника, а в условии сказано , что этот центр лежит на пересечении высот, то в ΔDEF высоты DH и EK являются серединными перпендикулярами. Так как основания перпендикуляров лежат на серединах сторон, то они явл. ещё и медианами. То есть медианы треугольника DEF - это ещё и высоты. Это может быть только в равностороннем (правильном) треугольнике.
ΔDEF - равносторонний.
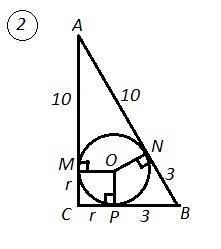
2) ΔАВС , ∠С=90°.
По теореме об отрезках касательных проведённых из одной точки , имеем
AM=AN=10 , BN=BP=3 , CM=CP=r - радиус вписанной окружности.
Р=30, P=10+10+3+3+r+r=26+2r ,
30=26+2r , 2r=4 , r=2
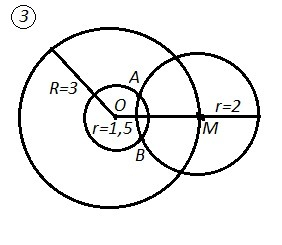
3) Точка М лежит на окр. радиуса R=3 см.
Точки, удалённые от т. М на расстояние 2 см, лежат на окружности с центром в точке М и радиуса r=2 см.
Точки, удалённые от центра первой окружности на расстояние 1,5 см , лежат на окружности с этим же центром , точкой О, и r=1,5 см.
Искомые точки будут принадлежать одновременно окружности с r=2 см и окружности с r=1,5 см.То есть это будут точки пересечения окружностей с центрами в точках М и О, с радиусами 2 см и 1,5 см - точки А и В. Задача имеет 2 решения.
Смотри рисунок.