ОТДАЮ ДУШУ, МАТЬ И 50 БАЛЛОВ Тому, кто всё распишет, объяснит, разжует и ответит на...

Предположим, есть уравнение:
$x^2+4x+10$

Мы должны сложить его часть в полный квадрат, то есть применить формулу

$a^2+2ab+b^2=(a+b)^2$

В нашем случае

$a=x$ ,
$2ab=4x\\2xb=4x\\2b=4\\b=2$

Значит, формула полного квадрата выглядит так:
$(a+b)^2=(x+2)^2$

Подставим её в исходное уравнение:
$x^2+4x+10=(x^2+4x+4)+6=(x+2)^2+6$ (так как $b^2=4$ , то от 10 остаётся 6, которое не сворачивается в полный квадрат, то есть остаётся за скобками).

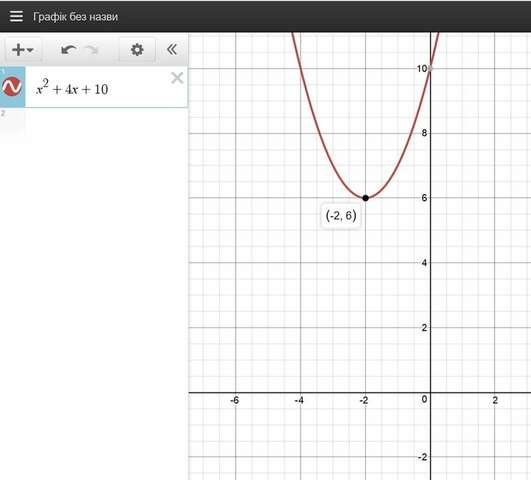
Из этой формулы видно, что абсцисса вершины параболы (то есть значение x, при котором функция принимает наименьшее значение) равна –2, а ордината вершины параболы (то есть значение функции в точке x=–2) равна 6.

Чтобы быстро применять этот метод, желательно помнить, как раскладываются выражения $(x+n)^2$ при $n$ равных от 1 до 10 хотя бы. А вообще при больших или дробных n искать вершину таким образом неудобно. Лучше находить абсциссу вершины параболы по формуле $-b/2a$ (a и b — коэффициенты уравнения: $ax^2+bx+c=0$ )

ОТДАЮ ДУШУ, МАТЬ И 50 БАЛЛОВ Тому, кто всё распишет, объяснит, разжует и ответит **...