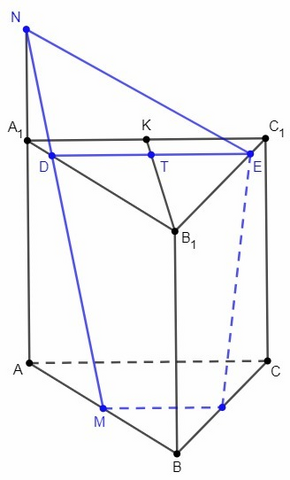
Точка N лежит на прямой AA1, следовательно в плоскости AA1B1. Точка M также лежит в этой плоскости. Плоскость NMT пересекает плоскость AA1B1 по прямой NM.
Пусть NM пересекает ребро A1B1 в точке D, а DT пересекает ребро B1C1 в точке E. Плоскость NMT пересекает грань A1B1C1 по отрезку DE.
Треугольники NA1D и NAM подобны (по двум углам; соответственные углы при A1B1||AB равны). A1D/AM =NA1/NA =1/3.
A1D составляет 1/3 от половины ребра (AM=AB/2), следовательно 1/6 от целого. Таким образом, точка D делит ребро B1A1 в отношении 5:1, считая от вершины B1. По условию точка T делит отрезок B1K в том же отношении 5:1, считая от вершины B1. Следовательно, по обратной теореме о пропорциональных отрезках, DT параллельна A1K (или DE||A1C1).
Треугольники B1DE и B1A1C1 подобны (по двум углам; соответственные углы при DE||A1C1 равны). DE/A1C1 =B1D/B1A1 =5/6.
DE= A1C1 *5/6 =18√6 *5/6 =15√6