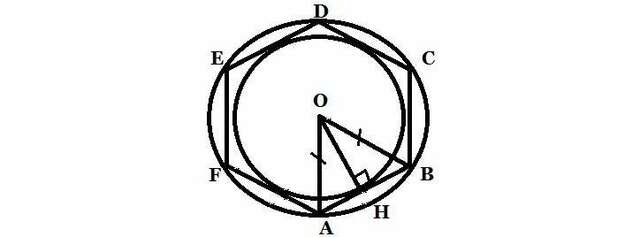
5.Итак, пусть будет вписан шестиугольник ABCDEF (см. приложение). Количество вершин многоугольника не влияет на решение))
Проведем радиусы OA и OB. Они будут равными как радиусы одной окружности. Проведем высоту OH, которая будет являться одновременно радиусом вписанной окружности и равна 3 по условию. Так как треугольник равнобедренный, то OH будет также являться медианой. Так как, AB - сторона многоугольника и основание треугольника AOB, равная 6√3, а OH - медиана, то AH = (6√3)÷2 = 3√3. Так как треугольник AOH - прямоугольник, а OA - гипотенуза, то воспользуемся т. Пифагора: OA = √((3√3)²+3²) = √36 = 6. Значит, радиус OA описанной окружности равен 6.