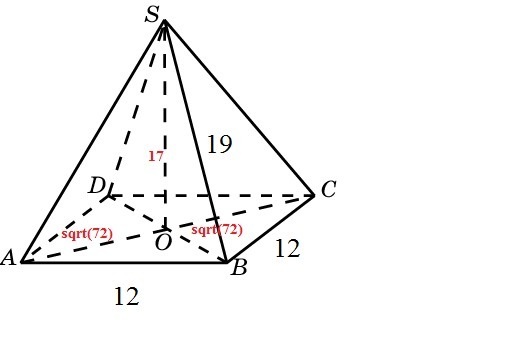
Так как пирамида правильная, в ее основании лежит квадрат, поэтому все стороны основания равны между собой. Возьмем две стороны:
AB = BC = 12.
Проведем диагональ AC и увидим прямоугольный треугольник.
AB, BC - катеты.
AC - гипотенуза.
AC² = AB² + BC² = 12² + 12² = 144 + 144 = 288.
AC = √288 = 2√72.
AC = DB - диагонали.
При этом в диагонали AC: AO = OC, а в диагонали DB: DO = OB.
Так как AO = OC = DO = OB, диагонали равны и делятся пополам:
AO = OC = DO = OB =  .
.
Возьмем треугольник SOB.
Зная гипотенузу SB и катет OB, найдем высоту SO:
SO² = SB² - OB² = 19² - √72 = 361 - 72 = 289.
SO = √289 = 17.
Ответ: 17.