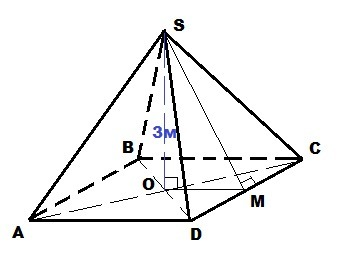
Площадь боковой поверхности правильной четырёхугольной пирамиды в четыре раза больше площади основания. Найти объём пирамиды, если её высота равна 3 м.
Правильная пирамида SABCD. В основании - квадрат. Высота опускается в центр квадрата - точку пересечения диагоналей.
Боковая поверхность в четыре раза больше площади основания и состоит из четырёх равных треугольников, значит, площадь одного треугольника (боковой грани) равна площади основания.

CD*SM/2 = CD²
SM = 2*CD²/CD = 2*CD
ΔSOM : ∠SOM = 90°; SO = 3 м; OM = 1/2 CD; SM = 2 CD
Теорема Пифагора
SM² = OM² + SO²
(2 CD)² = (1/2 CD)² + 3²
4 CD² = 1/4 CD² + 9 | *4
16 CD² = CD² + 36
15 CD² = 36
CD² = 36/15 = 2,4 м² - это площадь квадрата - основания S₀
Объём пирамиды
V = 1/3 * S₀ * SO = 1/3 * 2,4 * 3 = 2,4 м³