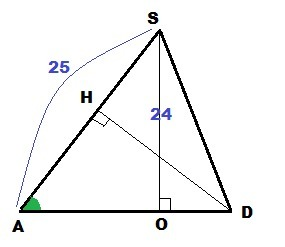
Расстояние между скрещивающимися прямыми - это их общий перпендикуляр.
Построить плоскость ASD. Прямая AS лежит в этой плоскости. Прямая CB пересекает эту плоскость в точке D ⇒
прямые AS и CB скрещивающиеся ⇒
нужно найти расстояние между прямыми AS и CB.
В ΔABC AD - высота ⇒ BC⊥AD ⇒ BC ⊥ (ASD) ⇒ BC⊥DH
Так как DH⊥AS и DH⊥BC ⇒
DH - расстояние между прямыми AS и CB
Высота правильной треугольной пирамиды опускается в центр вписанной и описанной окружности равностороннего треугольника основания. ⇒
R=AO радиус описанной окружности
r = OD радиус вписанной окружности
В равностороннем треугольнике R = 2r ⇒ AO = 2 OD
ΔASO прямоугольный, ∠AOS=90°. Теорема Пифагора
AO² = AS² - SO² = 25² - 24² = (25-24)(25+24)=49
AO = √49 = 7
sin∠A = SO/AS = 24/25 = 0,96
OD = 1/2 AO = 7/2 = 3,5
AD = AO + OD = 7 + 3,5 = 10,5
ΔAHD - прямоугольный, ∠AHD=90°
HD = AD*sin∠A = 10,5 * 0,96 = 10,08
Ответ: расстояние между скрещивающимися ребрами пирамиды 10,08