1) Исходное положение
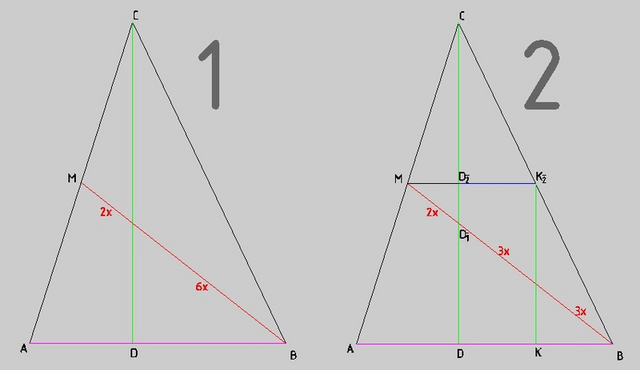
Медиана(красная) разрезана высотой на части 2х и 6x
2:6 = 1:3, так что всё по условию.
2) Построим среднюю линию треугольника АВС, параллельную стороне АВ
3) Построим семейство прямых, параллельных высоте СД, на расстоянии х друг от друга. Медина ВМ будет разбита на две части слева от высоты СД и на 6 частей справа.
Эти же прямые разобьют среднюю линию МК₂ в соотношении - две части слева от высоты и три части справа.
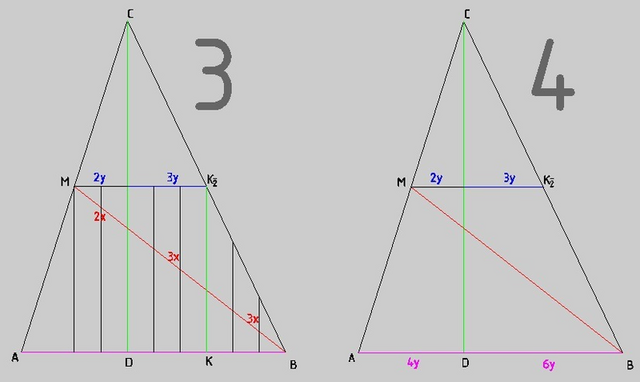
4) Средняя линия даёт треугольник, подобный исходному. И деление средней линии в отношении 2 к 3 даст в итоге деление основания треугольника высотой в отношении 4 к 6. Или, сократив, тоже получим 2:3
Средняя линия - уже на части 1y и 3/2y
Ну а основание - в соотношении 2y и 3y
Ответ - 2 к 3