Ваш первый вопрос:
------------------
Как доказать что медианы двух треугольников которые вписаны в произвольный шестиугольник пересекаются в одной точке?
------------------
и ответ - никак.
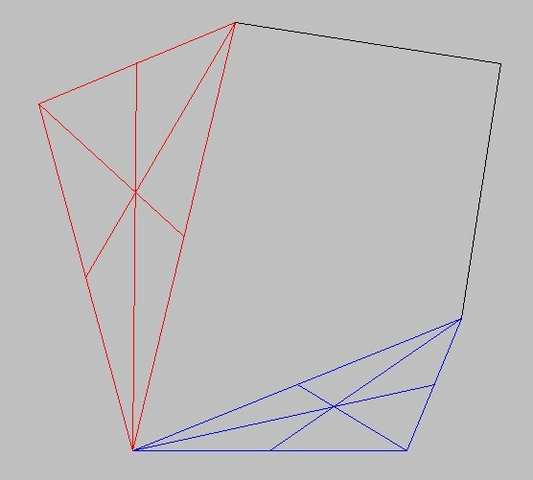
Медианы треугольников, построенных на сторонах шестиугольника НЕ ПЕРЕСЕКАЮТСЯ в одной точке.
Если рассматривать треугольники, просто вписанные в шестиугольник, с рёбрами, не совпадающими с рёбрами шестиугольника, то всё ещё хуже для пересечения медиан.
------------------------------------------------------
Ваш второй вопрос:
Как доказать что медианы двух треугольников, вершины которых совпадают с серединами сторона произвольного шестиугольника пересекаются в одной точке?
------------------
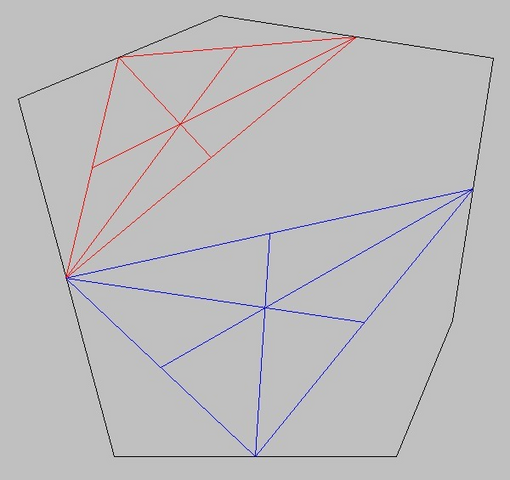
и снова - никак. медианы разных треугольников не пересекаются в одной точке
-----------------------------------------------------
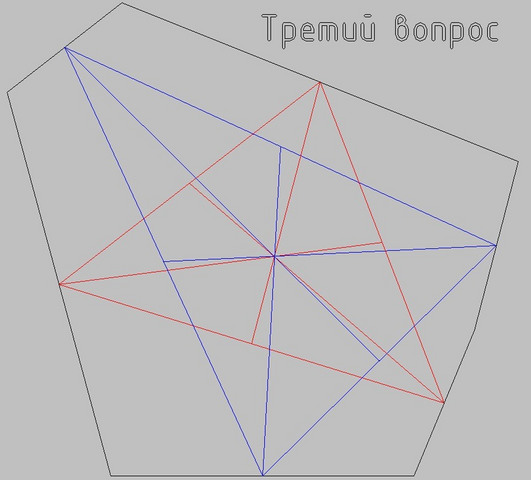
Теперь ваш третий вопрос, на случай, если вам снова захочется изменить условие задачи.
Есть точки вершин шестиугольника A₁..A₆
Есть точки середин рёбер шестиугольника B₁..B₆
На них построены два треугольника. B₁B₃B₅ и B₂B₄B₆
Точки пересечения медиан треугольников P и Q
Доказать, что P = Q
Воспользуемся координатым методом.
Координаты центра пересечения медиан первого треугольника
P = 1/3(B₁+B₃+B₅)
Для второго треугольника
Q = 1/3(B₂+B₄+B₆)
Координаты середин сторон шестиугольника
B₁ = 1/2(A₁+A₂)
B₂ = 1/2(A₂+A₃)
B₃ = 1/2(A₃+A₄)
B₄ = 1/2(A₄+A₅)
B₅ = 1/2(A₅+A₆)
B₆ = 1/2(A₆+A₁)
И координаты P и Q, выраженные через вершины шестиугольника
P = 1/3(1/2(A₁+A₂)+1/2(A₃+A₄)+1/2(A₅+A₆)) = 1/6(A₁+A₂+A₃+A₄+A₅+A₆)
Q = 1/3(1/2(A₂+A₃)+1/2(A₄+A₅)+1/2(A₆+A₁)) = 1/6(A₁+A₂+A₃+A₄+A₅+A₆)
Готово :)
P = Q