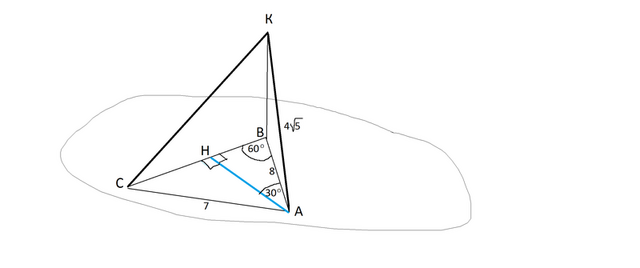
Из точки к плоскости проведены две наклонных. Длина одной из них равна 4√5, а длина ее проекции - 8 см. Угол между проекциями наклонных равен 60 градусов, а длина отрезка, соединяющего основания наклонных равна 7 см. Найдите длину второй наклонной.
-----------------------------------
Сделаем рисунок.
На плоскости получился треугольник.
Обозначим его вершины АВС.
Точку, удаленную от плоскости и в которой соединяются наклонные,
обозначим К.
Для того, чтобы найти наклонную КС, нужно знать КВ и ВС, которые являются катетами прямоугольного треугольника КВС ( КВ перпендикулярна к плоскости и проекциям наклонных).
КВ=√(АК²-АВ²)=√(80-64)=
4 см
В треугольнике АВС проведем высоту АН
Угол АВН=30 градусов.
ВН как катет прямоугольного треугольника АВН, противолежащий углу АВН, равен АВ:2=
4см
= АВ*cos60=8√3)
:2=
4√3
Из треугольника АНС найдем НС
НС(АС²-АН²)=√(49-48)=
1см
ВС=ВН+НС=
5см
Из прямоугольного треугольника КВС найдем нужную длину наклонной КС.
КС=√(КВ²+ВС²)=√(16+25)=√41