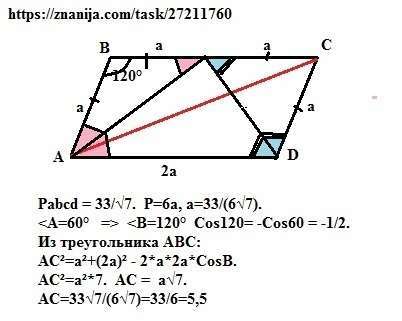
Биссектрисы углов параллелограмма отсекают от него равнобедренные треугольники (свойство). Причем в нашем случае они пересекаются на стороне ВС. Примем боковую сторону параллелограмма за "а". Следовательно Сторона ВС=2*а, а периметр параллелограмма тогда равен 6а=33/√7. а=.33/(6√7).
Угол В =120° (так как углы, прилежащие к одной стороне параллелограмма в сумме равны 180°). Cos120°= - Cos60° =-1/2.
тогда по теореме косинусов из треугольника АВС имеем:
АС²=а²+4а²+2*а*2а*(1/2) = а²*7. АС=а*√7. АС=33*√7/(6√7) =33/6 = 5,5.
Ответ: АС=5,5.