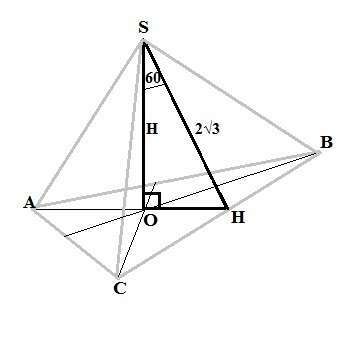
Угол между высотой и апофемой правильной треугольной пирамиды равен 60°. Найдите объем пирамиды, если апофема равна 2√3.
Высота пирамиды (катет) лежит против угла 30°, значит она равна половине апофемы (гипотенуза).
H=√3.
1/3 высоты основания (высота правильного треугольника - его медиана и делится центром О в отношении 2:1, считая от вершины) лежит в этом же треугольнике против угла 60° и равна 2√3*√3/2=3. Значит h=9.
Из формулы для правильного треугольника: h=(√3/2)*a находим сторону основания: а=2h/√3 =6√3. => So=(√3/4)a²=27√3.
Объем пирамиды
V=(1/3)*So*H=(1/3)*27√3*√3=27 ед².