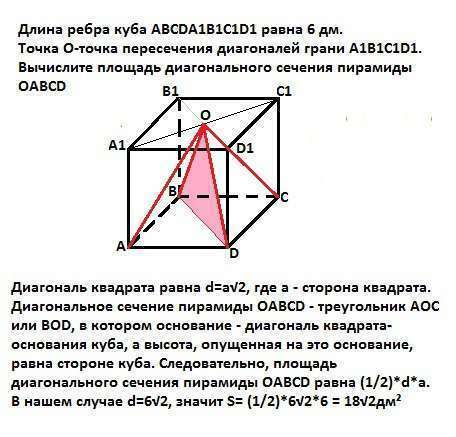
Диагональ квадрата равна d=а√2, где а - сторона квадрата.
Диагональное сечение пирамиды ОАВСD - треугольник АОС или ВОD, в котором основание - диагональ квадрата-основания куба, а высота, опущенная на это основание, равна стороне куба.
Следовательно, площадь диагонального сечения пирамиды ОАВСD равна
S=(1/2)*d*a.
В нашем случае d=6√2, значит S= (1/2)*6√2*6 = 18√2дм²
Ответ: площадь равна 18√2дм²